مدل سازی ریاضی قبلاً به عنوان روشی برای پرورش بیشتر گشودگی شناختی، در کلاس های ریاضیات شناخته می شد و مورد استفاده قرار می گرفت. مدل سازی ریاضی بیشتر شامل مسائل باز می شود تا مسائل بسته. مسائل باز یعنی مسائلی که بیش از یک راه حل برای آن ها وجود دارد. مسائل مطرح شده پیچیده و مسائل زندگی واقعی با کمک مدل های ریاضی قابل حل هستند. مسائلی از این نوع دانش آموزان را برای ایجاد ارتباط بین دنیای واقعی و ریاضیات و بالعکس از طریق آن چه به عنوان «چرخه مدل سازی» شناخته می شود، به چالش می کشد. برای درک چگونگی تفاوت یک تمرین مدل سازی با تمرین های معمول ارائه شده در کلاس های ریاضی، دو مثال زیر را در نظر بگیرید:
- تمرین سنتی: در روز خانواده در نمایشگاه، یک سواری بر روی ترن هوایی 4 یورو قیمت دارد. اگر مادر «تیم» 20 یورو به او بدهد، «تیم» چند بار می تواند سوار ترن هوایی شود؟
- تمرین مدل سازی: خانواده ای که در هامبورگ زندگی می کنند قصد دارند سفری را به یک پارک تفریحی انجام دهند. آن ها دو انتخاب دارند: یا پارک «دام» در هامبورگ یا «هایدپارك» در نزدیكی شهر سلتائو. کدام انتخاب بهترین انتخاب برای خانواده است؟ دلایل خوبی را برای این انتخاب ارائه دهید.
تمرین اول نیاز به یک محاسبه بسیار ساده دارد که منجر به نتیجه ای بدون ابهام می شود: 5= 4÷20. پاسخ صحیح این است: «تیم» می تواند پنج بار سوار ترن هوایی شود. فرقی نمی کند که تیم واقعاً پنج بار سوار ترن هوایی شود، یا این که آیا وی واقعاً 20 یورو در این راه خرج خواهد کرد یا نه. محاسبه صحیح است حتی اگر تمرین بی معنی باشد. از طرف دیگر، تمرین مدل سازی در یک زمینه بزرگ تر روایی داستانی جاسازی شده است. تکمیل تمرین مدل سازی مستلزم این است که کودکان زمینه بیشتری از مسأله را درک کنند، آن را شرح دهند و پارامترهای خاص خود را برای یافتن راه حل ایجاد کنند. آن ها باید این موارد را مشخص کنند: خانواده چند عضو دارد؟ میزان پول موجود برای سفر چه قدر است؟ چه روزی قرار است سفر انجام شود؟ خانواده قصد دارند چگونه به پارک بروند؟ و هزینه های مربوط به آن. آیا می خواهند نهار را در پارک بخورند یا نه و هزینه های مربوط به آن و سوار چه چیز هایی می خواهند بشوند. این نوع از تمرین باز، پیچیده، واقع بینانه، معتبر و با کمک ریاضیات قابل حل است. علاوه بر این، حل آن و مقایسه راه حل های مختلف مستلزم گفت و گو در بین دانش آموزان است.
در این مقاله از کار مدل سازی استفاده شده است و نحوه کار چرخه مدل سازی بر اساس این کار نشان داده شده است:
یک روز زمستانی که معلمان و کودکان به مدرسه خود می رسند، متوجه می شوند که کسی با استفاده از زور وارد مدرسه شده است. ردپایی در برف وجود دارد که احتمالاً توسط دزد ایجاد شده است. به منظور بررسی این جنایت، پلیس می خواهد مدرسه را طناب کشی کند تا دیگر کسی نتواند وارد آن شود.
- پلیس برای تعطیل کردن مدرسه به چه مقدار طناب احتیاج دارد؟
- با تشخیص از روی ردپای به جا مانده، قد سارق چه قدر بوده است؟
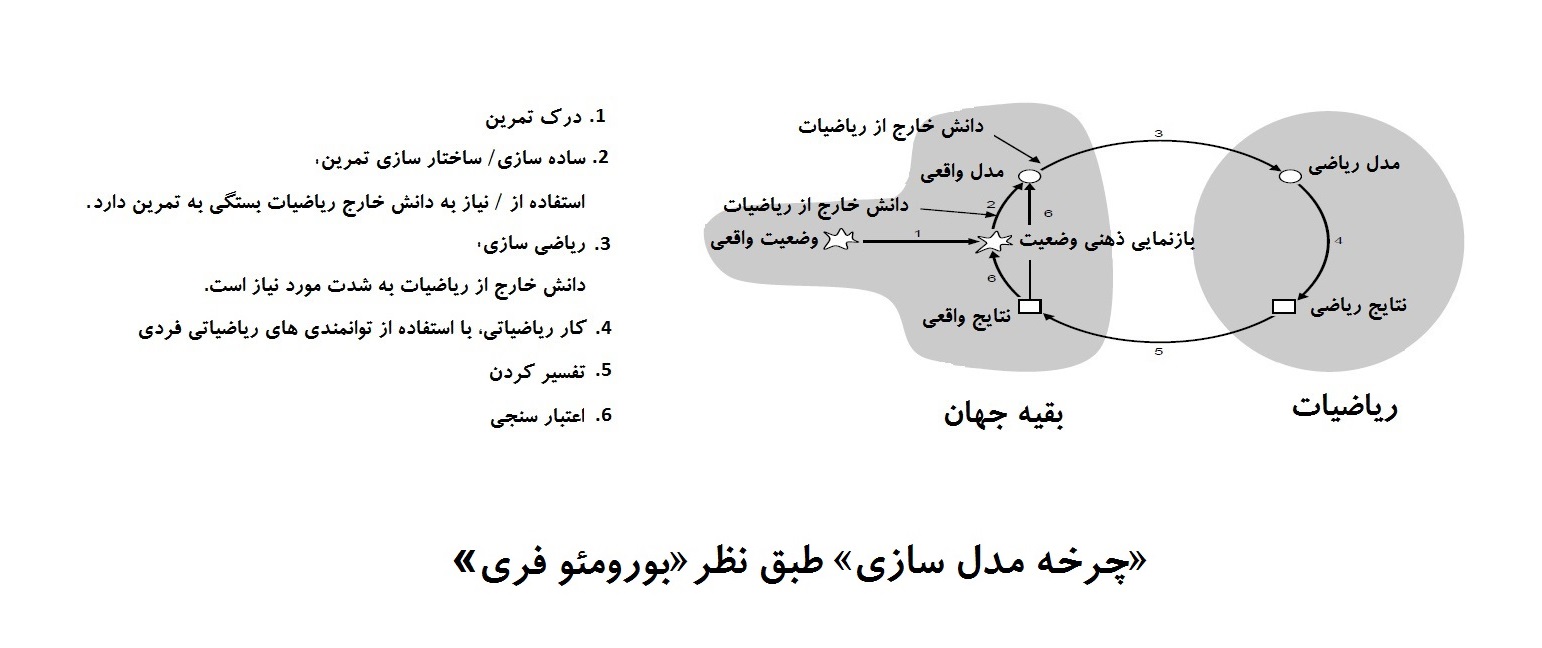
وضعیت واقعی در چرخه که در شکل نشان داده شده است، می تواند به شکل های مختلف به کودکان ارائه شود؛ به عنوان مثال در فرم نوشتاری یا به عنوان تصویر. در این مورد وضعیت به صورت داستان ارائه شده است. مسائل مطرح شده در این وضعیت، تعیین مقدار دقیق طناب مورد نیاز برای تعطیل کردن مدرسه توسط پلیس و تعیین مقدار قد سارق است. مرحله دوم چرخه، به اصطلاح بازنمایی ذهنی وضعیت است که در سطح ناخودآگاه اتفاق می افتد، اما همان طور که از تحقیقات تجربی می دانیم، برای درک مسأله، لازم است که کودکان وضعیت داده شده را تصور و تجسم کنند. در این مسأله بخصوص این بدان معنی است که کودکان باید ساختمان مدرسه خود و طناب را تصور کنند. شاید آن ها همچنین سرایدار، درب شکسته و پلیس را تصور کنند. این فرصتی برای انواع مختلف مشارکت را فراهم می کند.
سپس دانش آموزان مسأله را ساده می كنند و فرضیات را مطرح می كنند. در مورد حاضر، آن ها باید تصمیم بگیرند که کدام بخش از ساختمان مدرسه باید تعطیل شود، مثلاً کل ساختمان یا تنها بخشی از آن. برای انجام این کار، کودکان باید با نقشه کف ساختمان سر و کار داشته باشند و آن ها باید در مورد مقیاس و اندازه گیری دانش کسب کنند و یا به کار گیرند. مرحله بعدی ایجاد یک مدل ریاضی مبتنی بر این فرضیات است. این کار به چندین روش مختلف قابل انجام است. یک روش این است که به طور مستقیم طول طناب مورد نیاز بر اساس نقشه کف را تعیین کنند، مقادیر را جمع کنند و سپس این مقدار را به متر یا واحد های استاندارد دیگر تبدیل کنند. توانمندی های ریاضی مورد نیاز برای انجام این مرحله شامل جمع کردن، ضرب کردن، سر و کار داشتن با چندین واحد مختلف اندازه گیری و تبدیل آن ها به یکدیگر است. بسته به فرضیاتی که بچه ها مطرح می کنند، نتیجه ریاضی ممکن است 8 متر، در صورت بسته شدن ورودی های اصلی و جانبی، تا 350 متر، در صورت محصور بودن کل مدرسه، متغیر باشد. دانش آموزان باید نتایج خود را تفسیر کنند و سپس تصمیم بگیرند که آیا نتایج آن ها واقع بینانه است یا نه. این فرآیند سنجش و ارزیابی نتایج، اعتبارسنجی نامیده می شود. اگر کودکان به این نتیجه برسند که نتایج آن ها واقع بینانه نیست، مجبورند روند مدل سازی خود را دوباره ارزیابی کنند. در مطالعه حاضر، مراحل اوليه اين روش در گروه های كوچك انجام شده، در حالی كه اعتبارسنجی آن در بحثی با شرکت تمام اعضاء انجام شده است. هر دو بخش به گفت و گو نیاز دارند.
برای قسمت دوم تمرین مدل سازی با توجه به اندازه دزد، به کودکان طرح کلی ردپا روی یک کاغذ داده شد و از آن ها خواسته شد كه ردپای واقعی و دزدی را كه آن را ایجاد كرده تصور كنند. شاید آن ها نوع کفشی را که چنین رد پایی را ایجاد کرده است، نیز تصور کنند. سپس آن ها باید تصمیم بگیرند که چه اندازه گیری هایی لازم است. برای حل این مسأله، آن ها باید رابطه بین اندازه کفش و اندازه بدن را تخمین بزنند و آن را بر روی طرح ردپا اعمال کنند. برای این کار ممکن است این رابطه را در یکی از اعضای گروه خود اندازه بگیرند و یا مقدار متوسط به دست آمده از اندازه گیری چند نفر مختلف را تعیین کنند. به هر حال، یک رابطه ریاضی بین اندازه کفش و اندازه بدن تعیین می شود و رابطه به دست آمده برای ردپایی که به آن ها داده شده و طول آن 32 سانتی متر است، به کار برده می شود. سپس با استفاده از جبر می توانند اندازه سارق را تخمین بزنند. با فرض این که رابطه بین اندازه کفش و اندازه بدن 1: 6 باشد، نتیجه ریاضی 192= 32*6 سانتی متر خواهد بود. در واقعیت، اندازه یک فرد با ردپای متناظر با اندازه کفش اروپایی 46 (طول 32 سانتی متر)، می تواند بین 180 تا 200 سانتی متر باشد.
منبع:
http://journal.viterbo.edu/index.php/atpp/article/view/1105/917
مترجم: سهیلا جعفری
 فلسفه برای همگان
فلسفه برای همگان







